Articles
Fine-Tuning Your Risks By Dirk Vandycke

In this second of a two-part series on managing risk, we look at how to overcome the disadvantages of diversification. (Read Part 1) In part 1, it became clear that we need to bring profits and total return into the equation to evaluate the effects of diversification. However, it’s necessary to look beyond its common risk-lowering incentive and gain a more holistic view of diversification. While the advantages on the risk side are beneficial to all traders, from expert to layman, you mustn’t be blind to the disadvantages, mostly on the profit side. Diversification will spread risk, and hence lower it, but at the cost of averaging your returns. Let’s see if we can put this knowledge into practice.
Diversification vs. Concentration
Statistical expectancy tells us we have more control over the average size of winners and losers than over how frequently they occur. But frequency plays a role in profitability, so instead of trying to increase the numbers of winners while decreasing the number of losers, perhaps you should shift your focus to minimizing the size of losers and maximizing the size of winners. Cutting losses and riding winners is mathematically represented by expectancy. Shifting your resources so you have fewer winners will tend to concentrate your portfolio instead of spreading it. But how do you maximize profits with fewer winners? One way to do that is to add to winning positions, which would accelerate the speed of your winners and bring you higher profits. You can take an even bigger piece of the portfolio pie as a consequence.
Geometrical growth or power laws in mathematics tell us that diversification decreases average returns. Say you have nine winners of 2% and one winner of 30%. Average return in such a case would be a meager 4.50% using the following calculation:
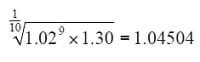
That one big winner increases the average return of the 2% winners by only 1.15%. If diversification didn’t decrease average and overall return, or if the effect is negligible, it means that the original returns must be similar. In such a case, the only thing diversification did was perhaps increase transaction costs, which contributed to lowering the return. If diversification is counterproductive to expectancy, then concentration could be a valid option. To determine if it is a valid option, I ran a Monte Carlo simulator on a database of thousands of stocks. I monitored the performance of these stocks over the last decade and over different market conditions.
The Test Portfolios
Each test included a portfolio of 13 randomly selected stocks over a specific time period, with the initial capital divided between all stocks. I had the computer run two copies of each portfolio. One was the homogenous diversified portfolio, which acted as a reference for comparison purposes. The other copy of the portfolio, the pruning portfolio, pruned the diversification and gradually morphed into a portfolio containing just one stock. The pruning portfolio placed a three ATR trailing stop for all positions. Once a position was stopped out, the cash from that position would get distributed evenly over the remaining holdings in the portfolio, thus adding to your positions. Eventually, there would only be one position holding 100% of all portfolio resources. Once this last position was stopped out, I compared the net return of both portfolios. The time period used was dictated by when the last stock of the pruning portfolio was stopped out.
Suggested Books and Courses About Psychology and Risk Management
Here Are The Results
The average return of all test portfolios is depicted in Figure 1. Each of the gray lines on the chart represents the average equity curves of all 13 portfolio holdings. Note that some stocks stayed in the portfolio longer than others. The solid red line is the equity curve of the pruning portfolio and the dashed green line represents the homogenous diversified portfolio. Clearly, concentrating funds by holding onto the winners seems to be the superior method. Note also that the return on the pruning portfolio is higher by 2.36% than that of the homogenous diversified portfolio. It may seem like a small edge, but the pruning portfolio had to make several artificial costs during the concentration process.
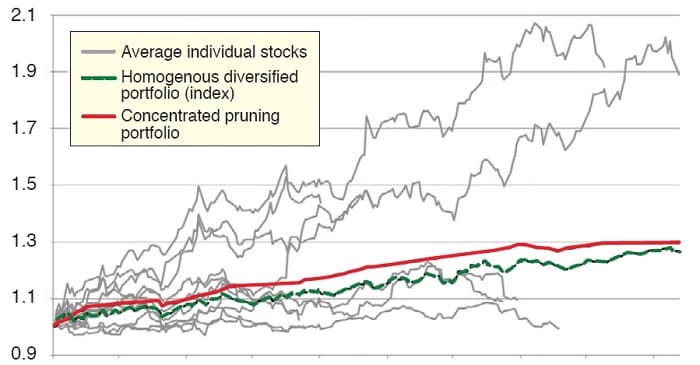
FIGURE 1: HOMOGENOUS DIVERSIFIED PORTFOLIO VS. PRUNING PORTFOLIO. The gray lines show the average returns of each of the stocks up to the point at which they got stopped out. The solid red line represents the pruning portfolio whereas the dashed green line represents the homogenous diversified portfolio.
Keep in mind that a concentrated portfolio can start with three or four stocks and have only one exit, which would reduce your transaction costs. Realistically, you would probably encounter fewer costs in the pruning portfolio than in the reference portfolio, and that would increase the return of the pruning portfolio.
Going Against Common Advice
Most people would think that eliminating the spreading of risks in order to lower average risk is not practical. Imagine holding 180% of your portfolio—you’re obviously using margin—in one position. Say this position opened 40% lower the next day on after-the-close news from the day before. No stop will protect you there. You’re trapped and bound to lose 72% of your total equity on a juicy margin call.
First of all, no one in his right mind would start out a position using 180% of his total capital. You would only get there by adding to or by scaling in winning trades. It’s likely that the current position has a nice profit and the current price is a safe distance away from the entry price. A simple technique to cope with this problem is to sell a portion or the entire position, and use the cash from the sale to purchase call options. Instead of holding, for example, 900 shares worth $30 apiece, you could sell the shares and have $27,000 in cash. You could then purchase 30 long- to medium-term call contracts for $3,000, which is only 11.11% of the original position. This cuts your downside to a fraction of what it was. The most you can lose now is the premium.
Shifting your resources so you have fewer winners will tend to concentrate your portfolio instead of spreading it.
Alternative Strategies
There are several other techniques you can apply to make up for losses in the markets. Of course, that would take up an entire article in itself or maybe even a book. My point is to encourage you to look for different ways to minimize your risks instead of following age-old strategies such as diversification. More tools are available to us these days that allow us to fine-tune our risk management strategies. Seek them out and take advantage of them.
Dirk Vandycke has been actively and independently studying the markets since 1995 with a focus on technical analysis, market dynamics, and behavioral finance.




